(a) ET = 18 and WE = 12
(b) FA = 16/3
HF = 8/3
ET = 8
WE = 4
Step-by-step explanation:
WT = 30 ( WE + ET = 30)
WE = 30 - ET
2FA = 3HF
FA = 3/2HF
WE =?, ET = ?
Line WH, EF and TA are parallel to each other.
(a)
ΔWTA and ΔWHA are congruent to each other
Therefore, by congruency
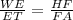
So,
30 - ET/ ET = HF / 3/2HF
30 - ET / ET = 2HF / 3HF
30 - ET / ET = 2/3
On solving the above equation we get, ET = 18
WE = 30 - ET
WE = 30 - 18 = 12
Therefore, ET = 18 and WE = 12
(b)
HA = 8 ( HF + FA = 8)
HF = 8 - FA
WT = 12 ( WE + ET = 12 )
WE = 12 - ET
GA = 2WG
HF, WA, WE, ET = ?
ΔWHA and ΔGFA are congruent
So,
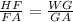
8 - FA / FA = WG / 2 WG
On solving the above equation we get,
FA = 16/3
HF + FA = 8
HF + 16/3 = 8
HF = 8/3
ΔWTA and ΔWEG are congruent
So,
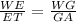
12 - ET / ET = WG / 2WG
On solving the above equation, ET = 8
WE = 12 - ET
WE = 12 - 8
WE = 4
Therefore, FA = 16/3
HF = 8/3
ET = 8
WE = 4