Answer:
200 million years
Step-by-step explanation:
The equation that describes the decay of a radioactive isotope is
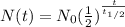
where
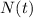 is the amount of radioactive isotope left at time t
is the amount of radioactive isotope left at time t
 is the initial amount of isotope
is the initial amount of isotope
 is the half-life of the sample
is the half-life of the sample
In this problem, the ratio between unstable isotope and daughter isotope is 1:15; this means that
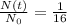
Because the "total proportion" of original sample was 1+15=16.
Also we know that the half-life is
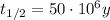
So we can re-arrange the equation to find t, the age of the rock:

So, 200 million years.