Question

A 12,500 N alien UFO is hovering about the surface of Earth. At time , its position can be given as () = ((0.24 m/s^3)^3 + 25 m)i^ ((4.2 m/s))j^+ (−(0.43 m/s^3)^3 + (0.8 m/s^2)^2)k^. What is the net force acting on the UFO at time = 2 s? Express your answer in vector format. What is its magnitude?

Answer 1

a)
`F=(3675i-4543k)N`

b) 5843 N

Step-by-step explanation:

a)

The position of the UFO at time t is given by the vector:

`r(t)=(0.24t^3+25)i+(4.2t)j+(-0.43t^3+0.8t^2)k`

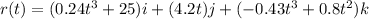
Therefore it has 3 components:

`r_x=0.24t^3+25\\r_y=4.2t\\r_z=-0.43t^3+0.8t^2`

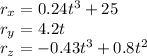
We start by finding the velocity of the UFO, which is given by the derivative of the position:

`v_x=r'_x=(d)/(dt)(0.24t^3+25)=3\cdot 0.24t^2=0.72t^2\\v_y=r'_y=(d)/(dt)(4.2t)=4.2\\v_x=r'_z=(d)/(dt)(-0.43t^3+0.8t^2)=-1.29t^2+1.6t`

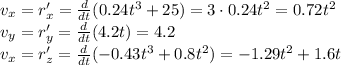
And then, by differentiating again, we find the acceleration:

`a_x=v'_x=(d)/(dt)(0.72t^2)=1.44t\\a_y=v'_y=(d)/(dt)(4.2)=0\\a_z=v'_z=(d)/(dt)(-1.29t^2+1.6t)=-2.58t+1.6`

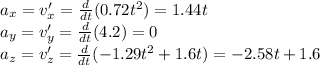
The weight of the UFO is W = 12,500 N, so its mass is:

`m=(W)/(g)=(12500)/(9.8)=1276 kg`

Therefore, the components of the force on the UFO are given by Newton's second law:

`F=ma`

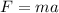
So, Substituting t = 2 s, we find:

`F_x=ma_x=(1276)(1.44t)=(1276)(1.44)(2)=3675 N\\F_y=ma_y=0\\F_z=ma_z=(1276)(-2.58t+1.6)=(1276)(-2.58(2)+1.6)=-4543 N`

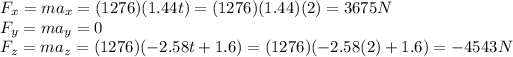
So the net force on the UFO at t = 2 s is

`F=(3675i-4543k)N`

b)

The magnitude of a 3-dimensional vector is given by

`|v|=√(v_x^2+v_y^2+v_z^2)`

where

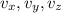`v_x,v_y,v_z` are the three components of the vector

In this problem, the three components of the net force are:

`F_x=3675 N\\F_y=0\\F_z=-4543 N`

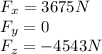
Therefore, substituting into the equation, we find the magnitude of the net force:

`|F|=√(3675^2+0^2+(-4543)^2)=5843 N`