The first time when the ball will reach a height of 20 feet is 0.42 seconds
Solution:
Given that,
The height of a ball thrown into the air after t seconds have elapsed is:
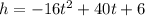
What is the first time, t, when the ball will reach a height of 20 feet?
Substitute h = 20
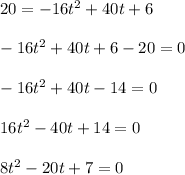
Solve by quadractic formula
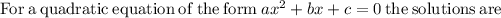
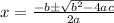
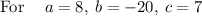
Rounding off we get,
t = 2.08 , t = 0.42
Thus the first time when the ball will reach a height of 20 feet is 0.42 seconds