Answer:
Compression of the spring: 0.18 m (downward)
Step-by-step explanation:
The forces acting on the block of wood are:
- The force of gravity, acting downward, of magnitude
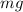 , where m = 5.32 kg is the mass of the block and
, where m = 5.32 kg is the mass of the block and
 is the acceleration due to gravity
is the acceleration due to gravity
- The force exerted by the spring, downward, of magnitude
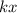 , where
, where
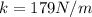 is the spring constant and
is the spring constant and
 is the elongation of the spring
is the elongation of the spring
- The buoyant force, upward, of magnitude
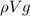 , where
, where
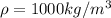 is the water density and V the volume of the block
is the water density and V the volume of the block
Since the block is in equilibrium, the net force is zero, so we can write
 (1)
(1)
We have to find the volume of the block first. We have:
m = 5.32 kg (mass)
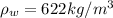 (wood density)
(wood density)
So, the volume is

So now we can re-arrange eq.(1) to find the elongation of the spring, x:
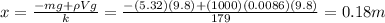
So, the spring is compressed by 0.18 m.