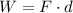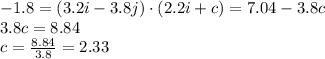A particle moves along a straight path through displacement while force acts on it. (Other forces also act on the particle.) What is the value of c if the work done by on the pa…

Question

asked Jul 14, 2021 168k views

1 Answer

Reptildarat · Answer 1 · 2021-07-19T01:29:22+0000

a) c = 1.85

b) c = 0.8

c) c = 2.33

Step-by-step explanation:

a)

The displacement of the particle is given by

d=2.2i+cj

While the force applied on the particle is

F=3.2i-3.8 j

So we have a problem in 2-dimensions.

The work done on the particle is given by the scalar product between force and displacement:

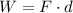$W=F\cdot d$ (1)

Here the work done on the particle is zero, so

W = 0

Therefore from eq(1) we find:

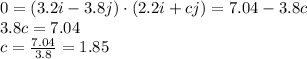
$0=(3.2i-3.8j)\cdot (2.2i+cj)=7.04-3.8c\\3.8c=7.04\\c=(7.04)/(3.8)=1.85$

b)

In this problem, the work done on the particle is

W=4.0 J

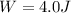
The force and displacement are still

d=2.2i+cj (displacement)

F=3.2i-3.8 j (force)

Therefore, by calculting the scalar product between force and displacement and equating it to the work done (4.0 J), we find:

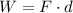
$W=F\cdot d$

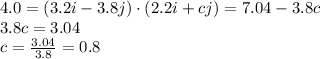
$4.0 =(3.2i-3.8j)\cdot (2.2i+cj)=7.04-3.8c\\3.8c=3.04\\c=(3.04)/(3.8)=0.8$

c)

In this problem instead, the work done on the particle is negative:

W=-1.8 J

As before, the force and displacement are

d=2.2i+cj (displacement)

F=3.2i-3.8 j (force)

And so again, we calculate the scalar product between force and displacement and we equate it to the work done on the particle, -1.8 J.

Doing so, we find:

$W=F\cdot d$

$-1.8=(3.2i-3.8j)\cdot (2.2i+c)=7.04-3.8c\\3.8c=8.84\\c=(8.84)/(3.8)=2.33$