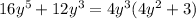Answer:
The expressions that completely factored are:
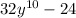 = 8(
= 8(
 ) ⇒ 2nd
) ⇒ 2nd
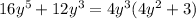 ⇒ 4th
⇒ 4th
Explanation:
Complete factorization means the terms in the bracket has no common factor
∵ The expression is 18y³ - 6y
- Find the greatest common factor of the numbers and the variable
∵ The greatest common factor of 18 and 6 is 6
∵ The greatest common factor of y³ and y is y
∴ The greatest common factor is 6y
- Divide each term by 6y to find the terms in the bracket
∴ 18y³ - 6y = 6y(3y² - 1) ⇒ not the same with the answer
∵ The expression is
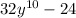
∵ The greatest common factor of 32 and 24 is 8
∴ The greatest common factor is 8
- Divide each term by 8 to find the terms in the bracket
∴
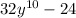 = 8(
= 8(
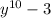 ) ⇒ the same with the answer
) ⇒ the same with the answer
∴ The expression
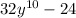 = 8(
= 8(
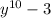 ) is completely factored
) is completely factored
∵ The expression is
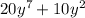
∵ The greatest common factor of 20 and 10 is 10
∵ The greatest common factor of
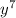 and y² is y²
and y² is y²
∴ The greatest common factor is 10y²
- Divide each term by 10y² to find the terms in the bracket
∴
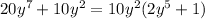 ⇒ not the same with the answer
⇒ not the same with the answer
∵ The expression is
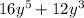
∵ The greatest common factor of 16 and 12 is 4
∵ The greatest common factor of
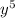 and y³ is y³
and y³ is y³
∴ The greatest common factor is 4y³
- Divide each term by 4y³ to find the terms in the bracket
∴
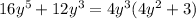 ⇒ the same with the answer
⇒ the same with the answer
∴ The expression
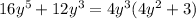 is completely factored
is completely factored
The expressions that completely factored are:
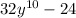 = 8(
= 8(
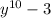 )
)