Question

2NB3 Components from three different manufacturers have been procured; 100 from Manufacturer A, of which 10% are defective; 300 from Manufacturer B, of which 5% are defective; and 500 from Manufacturer C, of which 20% are defective. We randomly select the shipment from one of the manufacturers and then randomly pick a component from it. (a) What is the probability that the selected component is defective

Answer 1

Explanation:

Hello!

There are 3 Manufacturers of 2NB3 components:

Manufacturer A

X₁: Number of defective components manufactured by A in a sample of 100.

From 100 components, 10% are defective.

Manufacturer B

X₂: Number of defective components manufactured by B in a sample of 300.

From 300, 5% are defective.

Manufacturer C

X₃: Number of defective components manufactured by C in a sample of 500.

From 500, 20% are defective.

These three variables are discrete and meet the criteria of the binomial experiment.

Binomial criteria:

1. The number of observation of the trial is fixed. n₁=100, n₂= 300 and n₃= 500

2. Each observation in the trial is independent, this means that none of the trials will have an effect on the probability of the next trial. There are two possible observations "success" and "failure" In this experiment, for the three variables the "success" is finding a defective piece-

3. The probability of success in the same from one trial to another. p₁= 0.10, p₂=0.05 and p₃= 0.20

X₁~Bi(n₁;p₁)

X₂~Bi(n₂;p₂)

X₃~Bi(n₃;p₃)

`P(X)= (n!)/((n-X)!X!)*(p)^x*(q)^(n-X)`

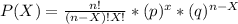
Manufacturer A

P(X₁=1)

`P(X_1=1)= (100!)/((100-1)!1!)*(0.1)^1*(0.9)^(100-1)= 0.00029`

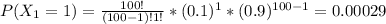
Manufacturer B

P(X₂=1)

`P(X_2=1)= (300!)/((300-1)!1!)*(0.05)^1*(0.95)^(300-1)= 0.0000033`

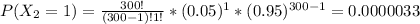
Manufacturer C

P(X₃=1)

`P(X_3=1)= (500!)/((500-1)!1!)*(0.2)^1*(0.8)^(500-1)= 0.000001`

I hope it helps!