Answer:
Check the attached graph below.
Explanation:
Let us consider the quadratic function
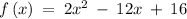
Observe that

As the value of
 is positive.
is positive.
i.e.
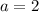
so, it would be an upward (U-shaped) graph.
Now, calculating the value of '
 '.
'.
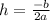
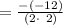

Then calculating
 (using
(using
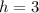 )
)
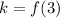
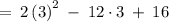
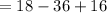

Now, plotting the graph, and the graph is attached below.
From the graph, it is clear that,
- The parabola vertex is

Please check the attached graph below.