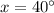Question

From the given figure find the value of x and y

Answer 1

The values of x and y are
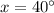`x=40^\circ` and
`y=70^{\circ`

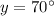
Step-by-step explanation:

From the given figure, we can see that
`\angle ABC = 70^\circ`

It is obvious from the figure that
`\angle ABC = \angle ACD`

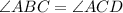
Since,
`\angle ABC = 70^\circ` and
`\angle A C D=y`

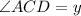
Thus, we have,

`\angle ABC = \angle ACD`

`70^(\circ)=y`

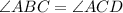
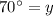
Thus, the value of y is
`y=70^{\circ`

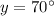
Now, we shall find the value of x.

From the figure, we can see that the sides AC and BC of
`\triangle ABC` are equal.

Hence, the
`\triangle ABC` is an isosceles triangle.

By isosceles triangle theorem,

"In any isosceles triangle, the angles opposite to the congruent sides are also congruent".

Hence, the congruent sides are AC and BC. The angles opposite to the congruent sides are
`\angle A \ and\ \angle B=70^(\circ)`

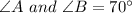
The value of x can be determined by adding all the angles in the
`\triangle ABC`

Thus, we have,

`\angle A+\angle B+\angle C = 180^\circ`

`70^(\circ)+70^(\circ)+x=180^(\circ)`

`140^(\circ)+x=180^(\circ)`

`x=40^(\circ)`

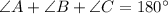
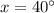
Thus, the value of x is
`x=40^\circ`