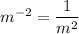Question

9

Apply index law three to simplify each of the following.
a
(m2)
b
6(p^)

Answer 1

• See the law and the hypothetical example below.

Step-by-step explanation:

The index law that you are dealing with is:

`(a^m)/(a^n)=a^(m-n)`

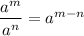
It is used when you have the quotient of powers with the same base.

To show you how to use that rule, let's work an example

Simplify:

`(9a(m^2))/(6b(m^4))`

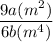
Factor 9 as 3² and 6 as 2×3:

`(3^2a(m^2))/(2* 3b(m^4))`

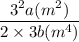
Group the factor with equal base:

`(a)/(2b)* (3^2)/(3)* (m^2)/(m^4)`

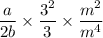
Use the index law:

`(a)/(2b)* {3^((2-1))}* m^((2-4))\\\\\\ (a)/(2b)*3* m^(-2)\\\\\\(3a)/(2bm^2)`

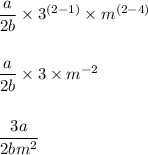
Note that it was used an additional rule:
`a^(-n)=(1)/(a^n)`

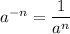
Thus,
`m^(-2)=(1)/(m^2)`