Answer:
(a) Mean = 72.1 Standard deviation = 6.14
(b) New Mean = 85.1 New Standard deviation = 6.14
Explanation:
We are given the scores on a 100-mark test of a sample of 80 students in a large school;
Score No. of students (f) X X*f
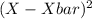
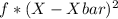
59 - 63 6 61 366 123.21 739.26
63 - 67 10 65 650 50.41 504.1
67 - 71 18 69 1242 9.61 172.98
71 - 75 24 73 1752 0.81 19.44
75 - 79 10 77 770 24.01 240.1
79 - 83 8 81 648 79.21 633.68
83 - 87 4 85 340 166.41 665.64
∑f = 80 ∑X*f = 5768 Total = 2975.2
(a) Mean of the above data, X bar =
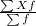 =
=
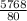 = 72.1
= 72.1
Standard deviation, s =
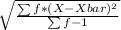 =
=
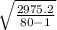 = 6.14
= 6.14
Therefore, mean and standard deviation of the scores of all students are 72.1 and 6.14 respectively.
(b) Now, a bonus of 13 points is to be added to these scores.
So, Mean will also increases by 13 points and due to this;
New Mean = 72.1 + 13 = 85.1
Adding 13 points to each score will not affect standard deviation and due to which New standard deviation is same as before of 6.14.