Question

Please I need this before 12pm

Answer 1

The required formula is:

`{\displaystyle \ a_(n)=a_(1)+(n-1)d}`

Explanation:

The total number of squares of the the first term = 4

The total number of squares of the the second term = 7

The total number of squares of the the third term = 10

so,

`a_1=4`

`a_2=7`

`a_3=10`

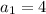
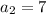
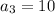
Finding the common difference d

`d=a_3-a_2=10-7=3`

`d=a_2-a_1=7-4=3`

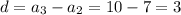
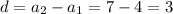
As the common difference 'd' is same, it means the sequence is in arithmetic.

So

If the initial term of an arithmetic progression is
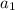`{\displaystyle a_(1)}` and the common difference of successive members is d, then the nth term of the sequence
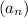`(a_n)` is given by:

`{\displaystyle \ a_(n)=a_(1)+(n-1)d}`

Therefore, the required formula is:

`{\displaystyle \ a_(n)=a_(1)+(n-1)d}`