Answer:
see the explanation
Explanation:
we know that
The volume of a cone is equal to
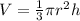
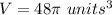
so
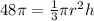
Simplify
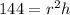 ----> equation A
----> equation A
step 1
Cone a
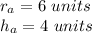
Verify
substitute the given values in equation A
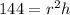
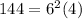
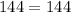 ---> is true
---> is true
step 2
Cone b
Assume the value of the radius and with the equation A calculate the value of the height
so
For
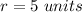
substitute in the equation A
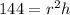
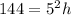
solve for h
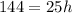
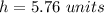
Verify
substitute the given values in equation A
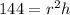
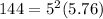
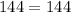 ---> is true
---> is true
The value of r and h satisfy the equation A, that means the volume of cone b is the same that volume of cone a