Answer:
P(caramel) = 3/10
P(raspberry) = 1/3
Explanation:
Given:
- Caramel chocolates = 3
- Raspberry chocolates = 3
- Fudge chocolates = 4
⇒ Total chocolates = 3 + 3 + 4 = 10
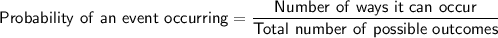

If the picked caramel chocolate is NOT replaced then:
- Caramel chocolates = 3 - 1 = 2
- Raspberry chocolates = 3
- Fudge chocolates = 4
- Total chocolates = 10 - 1 = 9
