Question

If the graph of f(x)= x^2+10x+k has two distinct zeros, find the value of k

please be clear and explain the reason. Thanks very much

Answer 1

The value of k must be less than 25

Explanation:

we have

`f(x)=x^2+10x+k`

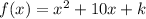
we know that

If the discriminant of a quadratic function is greater than zero, then the function has two distinct zeros

so

The discriminant D is equal to

`D=b^2-4ac`

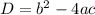
we have

`a=1\\b=10\\c=k`

`D=10^2-4(1)(k)\\D=100-4k`

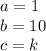
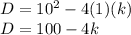
Remember that

`D> 0`

so

`100-4k> 0`

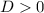
solve for k

`-4k> -100`

Divide by -4 both sides

`k< 25`

therefore

The value of k must be less than 25