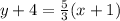Answer:
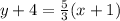
Explanation:
The equation in the point-slope form of a line is written as
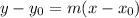 (1)
(1)
where
m is the slope of the line
 are the coordinates of a point on the line
are the coordinates of a point on the line
In this problem, we hate two points belonging to the line:
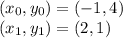
Therefore we can find the slope with the following equation:
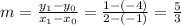
And by substituting
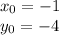 into eq(1), we find
into eq(1), we find