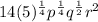Question

How do you simplify
`7\sqrt[4]{80pq^(2)r^(8) }`?

Answer 1

`14 ( 5)^{(1)/(4)} p^{(1)/(4)} q^{(1)/(2)} r^(2)`

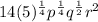
Explanation:

The expression to simplify in this problem is

`7\sqrt[4]{80pq^2r^8}`

Which can be rewritten as

`7(80pq^2r^8)^{(1)/(4)}`

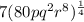
Or also as

`7\cdot 80^{(1)/(4)} \cdot p^{(1)/(4)} \cdot (q^2)^{(1)/(4)} \cdot (r^8)^{(1)/(4)}`

Now we can apply the following rule for the calculation of the power of a power:

`(a^m)^n = a^(m\cdot n)`

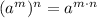
So we get:

`7\cdot 80^{(1)/(4)} \cdot p^{(1)/(4)} \cdot q^{(1)/(2)} \cdot r^(2)`

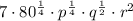
Which can therefore be rewritten as

`7\cdot (2^4\cdot 5)^{(1)/(4)} \cdot p^{(1)/(4)} \cdot q^{(1)/(2)} \cdot r^(2)`

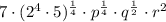
And so, we get

`7\cdot 2 \cdot ( 5)^{(1)/(4)} \cdot p^{(1)/(4)} \cdot q^{(1)/(2)} \cdot r^(2)`

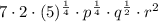
which can be finally rewritten as

`14 ( 5)^{(1)/(4)} p^{(1)/(4)} q^{(1)/(2)} r^(2)`