Question: Express
 in trigonometric form.
in trigonometric form.
Answer:
A few ways to express this is:
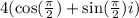
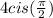
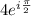
Choose the notation your class is using.
Explanation:
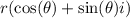 is trigonometric form.
is trigonometric form.
Distributing
 to terms inside the ( ) gives:
to terms inside the ( ) gives:
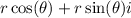 .
.
Our number has no real part so we are just trying to find
 and
and
 such that
such that
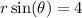 .
.
Since we want
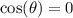 , we will have to
, we will have to
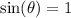 (or -1).
(or -1).
This happens at
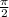 .
.
This means
 .
.
So while
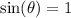 this forces
this forces
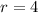
The trigonometric form is
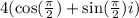 .
.
Some people like to express this as
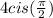 which is way shorter.
which is way shorter.
Some people might also express this as
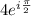 .
.