Question

Which of the following rational functions is graphed below?​

Answer 1

The correct option is D.

i.e.

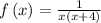`f\left(x\right)=(1)/(x\left(x+4\right))` is the correct option.

The correct graph is shown in attached figure.

Explanation:

Considering the function

`f\left(x\right)=(1)/(x\left(x+4\right))`

`\mathrm{Domain\:of\:}\:(1)/(x\left(x+4\right))\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<-4\quad \mathrm{or}\quad \:-4<x<0\quad \mathrm{or}\quad \:x>0\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-4\right)\cup \left(-4,\:0\right)\cup \left(0,\:\infty \:\right)\end{bmatrix}`

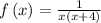
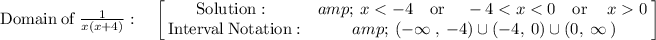
`\mathrm{Range\:of\:}(1)/(x\left(x+4\right)):\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)\le \:-(1)/(4)\quad \mathrm{or}\quad \:f\left(x\right)>0\:\\ \:\mathrm{Interval\:Notation:}&\:(-\infty \:,\:-(1)/(4)]\cup \left(0,\:\infty \:\right)\end{bmatrix}`

`\mathrm{Axis\:interception\:points\:of}\:(1)/(x\left(x+4\right)):\quad \mathrm{None}`

`\mathrm{Extreme\:Points\:of}\:(1)/(x\left(x+4\right)):\quad \mathrm{Maximum}\left(-2,\:-(1)/(4)\right)`

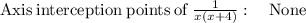
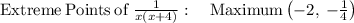
So, the correct graph is shown in attached figure.

Therefore, the correct option is D.

i.e.

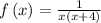`f\left(x\right)=(1)/(x\left(x+4\right))` is the correct option.