Question

On the basis of data from 1990 to 2006, the median income y in the year x for men and women is approximated by the equations given below, where x=0 corresponds to 1990 and y is in constant 2006 dollars. If these equations remain valid in the future, in what year will the median income of men and women be the same? Men: -236x + 2y = 56,939 Women: -838x + 3y = 41,655

Answer 1

The median income would be the same, based on these equations, in approximately 90.4 years time, which is around approximately in the year 2080

Explanation:

Given the approximate equations for men and women respectively:

`-236x + 2y = 56 939`

`-838x + 3y = 41 655`

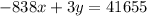
Where X stands for number of years and y stands for median. Since we are looking for the year, x, where the median, y, would be the same, then we have to rewrite both equations such that y would be the subject of the equations, why? So that, we can have an equation for the median income, and whenever the median income becomes equal, we would have a certain number years, X, that would happen, here is what I'm trying to say:

The first equation can be rewritten as:

`2y = 56 939 + 236x`

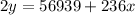
Dividing both sides by 2, we have:

`y = (1)/(2)(56 939 + 236x)`

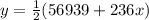
Similarly, from the second equation we have:

`3y = 41 655 + 838x`

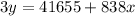
Dividing both sides by 3, we have:

`y = (1)/(3)(41 655 + 838x)`

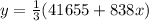
Now, we have the equations in terms of y, from both equations we can say:

`(1)/(3)(41 655 + 838x) = (1)/(2)(56 939 + 236x)`

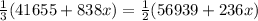
We have to solve for x, the number of years, in order to get when y, the median would be equal.

Multiply both sides of the last equation by 6 we get:

`2(41 655 + 838x) = 3(56 939 + 236x)`

Which gives:

`83 310 + 1 676x = 170 817 + 708x`

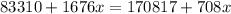
Collecting like terms we have:

`1 676x - 708x = 170 817 - 83 310`

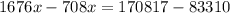
We then have:

`968x = 87 507`

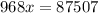
Dividing both sides of the last equation by 968

We get:

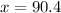`x = 90.4`(approximately)

Therefore the number years we need for the median income to be the same is approximately 90.4years which will fall around 2080. And that is the required answer.

Answer 2

X=$195.78

Y=$51571.95

This will be the same in the year 2006

Explanation:

-236x +2y =56939 ..eq1

-838x + 3y= 41655 ..eq2

Multiply eq1 by-3 and eq2 by 2 gives:

378x - 6y= -170817

-1676x +6y= 83310

Subtracting gives:

-1298x= -254127

Dividing with -1298

X= $195.78

Substituting the value of X in eq2

-236(195.78) + 2y= 56939

-46204.91 - 56939=-2y

103143.91/2=y

Y=$ 51571.95