Question

Pls show full working out

Answer 1

• Question 1a. i)
  `x=1.8m`

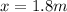
• Question 1a. ii)
  `Volume=27.6m^3`

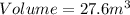
• Question 1b)
  `Volume=65.9m^3`

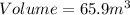
Step-by-step explanation:

Question 1 a. i) Find the value of x.

`tan(\theta )=\frac{opposite\text{ }leg}{adjacent\text{ }leg}`

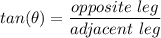
For the smalll triangle you can write:

`tan(\theta )=(x)/(1m)`

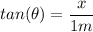
For tthe big triangle:

`tan(\theta )=(x+2.7m)/(2.5m)`

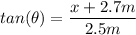
Substitute:

`(x)/(1m)=(x+2.7m)/(2.5m)`

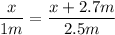
Solve for x:

`2.5x=x+2.7m\\\\2.5x-x=2.7m\\\\1.5x=2.7m\\\\x=2.7m/1.5\\\\x=1.8m`

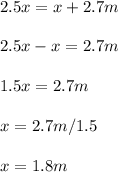
Question 1a ii) Find the volume of the frustrum

• Find the volume of a cone with height = 2.7m + 1.8m = 4.5m, and radius = 2.5m

Formula:

`Volume=(1/3)\pi * radius^2* height`

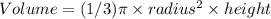
Substitute:

`Volume=(1/3)\pi * (2.5m)^2* 4.5m=9.375\pi m^3`

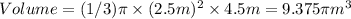
• Find the volume of a cone with heigth = 1.8m and radius = 1m

`Volume=(1/3)\pi * (1m)^2* 1.8m=0.6\pi m^3`

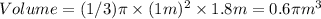
• Subtract the volume of the small cone from the volume of the big cone

`Volume\text{ }of\text{ }frustrum=9.375\pi m^3-0.6\pi m^3=8.775\pi m^3\approx 27.6m^3`

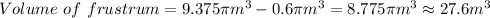
Question 1b. Calculate the volume of the bin

i) Upper frustrum

This is the same frustrum from the equation of above, thus ist volume is 27.6m³.

ii) Lower frustrum

`(x)/(2.0m)=(x+2.4m)/(2.5m)`

`2.5x=2(x+2.4m)\\\\2.5x=2x+4.8m\\\\0.5x=4.8m\\\\x=9.6m`

`Volume=(1/3)\pi * (2.5m)^2* (9.6m+2.4m)-(2.0m)^2* (9.6m)`

`Volume=38.3m^3`

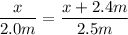
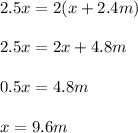
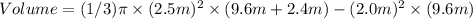
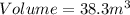
iii) Add the volume of the two frustrums

• 
  `Volume=27.6m^3+38.3m^3=65.9m^3`