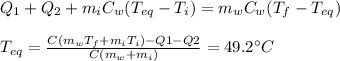Question

Calculate the final temperature of a mixture of 200.0 g of ice initially at -20.50 °C and 319.0 g of water initially at 91.50 °C.

Answer 1

`49.2^(\circ)C`

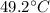
Step-by-step explanation:

As the ice is in contact with the water, heat is transferred from the water to the ice; part of the heat is used to bring the ice to its melting point (
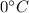`0^(\circ)C`), part is used to melt the ice, and the rest is used to increase the temperature of the ice (which is now melted) to the equilibrium temperature.

At the same time, the temperature of the water decreases to the equilibrium temperature.

The heat needed by the ice to reach the melting point is:

`Q_1=m_i C (T_f -T_i)`

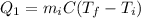
where

`m_i = 200.0 g` is the mass of the ice

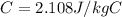`C=2.108 J/kg C` is the specific heat of ice

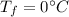`T_f=0 ^(\circ)C` is the final temperature

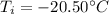`T_i=-20.50^(\circ)C` is the initial temperature

Substituting,

`Q_1=(200.0)(2.108)(0-(-20.50))=8643 J`

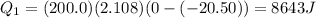
Then, the heat needed to melt the ice when it reached the melting point is

`Q_2=\lambda m_i`

where

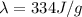`\lambda=334 J/g` is the specific latent heat of ice

Substituting,

`Q_2=(334)(200.0)=6680 J`

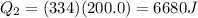
Now, the ice has completely melted, so it's now liquid water; the heat needed to reach the equilibrium temperature is

`Q_3=m_i C_w (T_(eq)-T_i)`

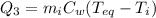
where

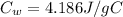`C_w=4.186 J/gC` is the specific heat of water

`T_(eq)` is the equilibrium temperature

`T_i=0^(\circ)C` is the initial temperature of ice

At the same time, the heat released by the 319.0 g of liquid water is

`Q_4=m_w C_w(T_f-T_(eq))`

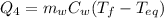
where

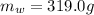`m_w=319.0 g` is the mass of the water

`T_f=91.50^(\circ)` is the initial temperature of the water

Since the total energy is conserved, we have:

`Q_1+Q_2+Q_3=Q_4`

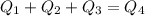
Therefore, substituting and re-arranging, we find the equilibrium temperature:

`Q_1+Q_2+m_i C_w(T_(eq)-T_i)=m_w C_w (T_f-T_(eq))\\\\T_(eq)=(C(m_w T_f+m_i T_i)-Q1-Q2)/(C(m_w+m_i))=49.2^(\circ)C`