Question

Assume that when with smartphones are randomly selected, 46% use them in meetings or classes. If 12 adult smartphone users are randomly selected, find the probability that fewer than 3 of them use their smartphones in meetings or classes.

Answer 1

The probability that fewer than 3 of them use their smartphones in meetings or classes is 0.03634

Explanation:

Apply binomial probability formula which is written as;

`P(X=x)=(n!)/(x!(n-x)!) *P^(x) *(1-P)^(n-x)`

where P=46% =0.46, n=12

For this case where you find the probability that fewer than 3 of them use their smartphones in meeting or classes, x=2,1,0

Evaluating binomial probability at x=2 will be;

`P(X=2)=(12!)/(2!(12-2)!) *0.46^2*(1-0.46)^(12-2) \\\\P(X=2)=(12!)/(2!10!) *0.2116*0.002108\\\\=66*0.2116*0.002108\\=0.02944`

P(X=2)=0.02944

Evaluate binomial probability at x=1

`P(X=1)=(12!)/(1!(12-1)!) *0.46^1*(1-0.46)^(12-1) \\\\P(X=1)=(12!)/(1!11!) *0.46*0.54^(11) \\\\P(X=1)=12*0.46*0.001138\\\\P(X=1)=0.006284`

P(X=1)= 0.006284

Evaluate binomial probability at x=0

`P(X=0)=(12!)/(0!(12-0)!) *0.46^0*(1-0.46)^(12-0) \\\\P(X=0)=(12!)/(1*12!) *0.46^0*0.54^(12) \\\\P(X=0)=1*1*0.0006148 =0.0006148`

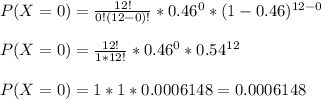
P(X=0)=0.0006148

Now for P(X<3)=P(X=2)+P(X=1)+P(X=10) =0.02944+0.006284+0.0006148

=0.0363388

=0.03634 (in 4 significant figures)