Question

Please Need help on these

Answer 1

Question # 3

Answer:

`x = 13.094`

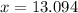
Explanation

Considering the exponential equation

`e^(x-9)-6=54`

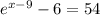
Solving the exponentiation equation

`e^(x-9)-6=54`

`\mathrm{Add\:}6\mathrm{\:to\:both\:sides}`

`e^(x-9)-6+6=54+6`

`e^(x-9)=60`

`\mathrm{If\:}f\left(x\right)=g\left(x\right)\mathrm{,\:then\:}\ln \left(f\left(x\right)\right)=\ln \left(g\left(x\right)\right)`

`\ln \left(e^(x-9)\right)=\ln \left(60\right)`

`\mathrm{Apply\:log\:rule}:\quad \log _a\left(x^b\right)=b\cdot \log _a\left(x\right)`

`\ln \left(e^(x-9)\right)=\left(x-9\right)\ln \left(e\right)`

`\left(x-9\right)\ln \left(e\right)=\ln \left(60\right)`

`\mathrm{Apply\:log\:rule}:\quad \log _a\left(a\right)=1`

`\ln \left(e\right)=1`

`x-9=\ln \left(60\right)`

`x=\ln \left(60\right)+9`

`x=13.094` ∵
`\ln \left(60\right)=4.094`

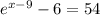
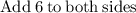
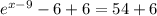
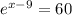
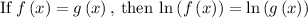
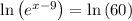
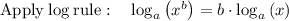
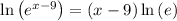
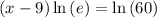
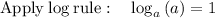
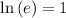
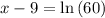
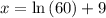
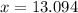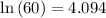
Therefore, x = 13.094

Question # 4

Answer:

`x=0.386`

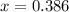
Explanation

Considering the exponential equation

`3e^(9x)-6=91`

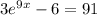
Solving the exponentiation equation

`3e^(9x)-6=91`

`\mathrm{Add\:}6\mathrm{\:to\:both\:sides}`

`3e^(9x)=97`

`\mathrm{Divide\:both\:sides\:by\:}3`

`(3e^(9x))/(3)=(97)/(3)`

`e^(9x)=(97)/(3)`

`\mathrm{If\:}f\left(x\right)=g\left(x\right)\mathrm{,\:then\:}\ln \left(f\left(x\right)\right)=\ln \left(g\left(x\right)\right)`

`\ln \left(e^(9x)\right)=9x\ln \left(e\right)`

`9x\ln \left(e\right)=\ln \left((97)/(3)\right)`

`\mathrm{Apply\:log\:rule}:\quad \log _a\left(a\right)=1`

`\ln \left(e\right)=1`

`9x=\ln \left((97)/(3)\right)`

`\mathrm{Divide\:both\:sides\:by\:}9`

`(9x)/(9)=(\ln \left((97)/(3)\right))/(9)`

`x=(\ln \left((97)/(3)\right))/(9)`

`x=(3.476)/(9)` ∵
`ln\left((97)/(3)\right)=3.476`

`x=0.386`

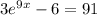
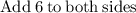
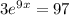
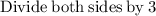
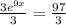
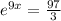
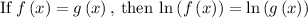
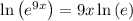
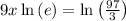
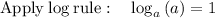
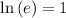
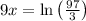
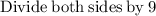
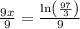
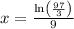
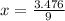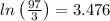
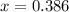
Therefore, x = 0.386