Answer:
The original fraction is equal to

Explanation:
Let
The fraction in the simplest form equal to

we know that
The denominator of a fraction in the simplest form is greater than the numerator by 1
so
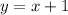 ----> equation A
----> equation A
If 4 is added to the numerator, and 3 is subtracted from the denominator, then the fraction itself is increased by 2 1/6
Remember that

so
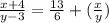 ----> equation B
----> equation B
substitute equation A in equation B
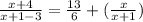
solve for x
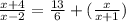
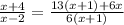
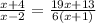
Multiply in cross
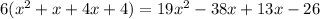
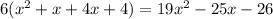

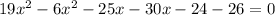

solve the quadratic equation by graphing
The solution is x=5
therefore
Find the value of y
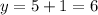
The original fraction is equal to
