Question

Four batsmen on a cricket team had a mean of 42.5 runs the other 7 batsmen had a mea of 18 what was the mean number of scored by the entire team rounded the nearest whole mumber

Answer 1

The mean score of the entire team is 26.909.

Explanation:

Given that four batsmen had a mean of 42.5.

Let
`$ \textbf{B}_{\textbf{i} $`, where
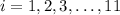`$ i = 1, 2, 3, \hdots, 11 $` denote the batsmen.

From the first statement, we have:

`$ (B_1 + B_2 + B_3 + B_4)/(4) = 42.5 $`

`$ \implies B_1 + B_2 + B_3 + B_4 = 42.5 * 4 = \textbf{170} $`

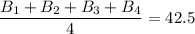
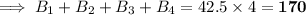
Therefore, the sum of the scores of the first four batsmen is 170.

Now, from the second statement we have:

`$ (B_5 + B_6 + B_7 + B_8 + B_9 + B_(10) + B_(11))/(7) = 18 $`

`$ \implies B_5 + B_6 + B_7 + B_8 + B_9 + B_(10) + B_(11) = 18 * 7 = \textbf{126} $`

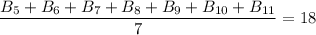
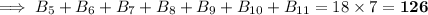
That is, the sum of the scores of the remaining 7 batsmen is 126.

Now, to calculate the average(mean) of the entire team, we add the individual scores and divide it by 11.

`$ \implies (B_1 + B_2 + B_3 + B_4 + B_5 + B_6 + B_7 + B_8 + B_9 + B_(10) + B_(11))/(11) = (170 + 126)/(11) $`

`$ = (296)/(11) $`

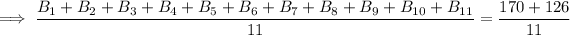
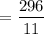
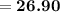`$ = \textbf{26.90} $` which is the required answer.