Answer:
Explanation:
Given that a quadratic function(polynomial of degree 2) passes through two points (1,5) and (3,7)
The function would be of the form

with if a>0 open up and if a<0 open down
Since passes through(1,5) and (3,7) these points satisfy the equation
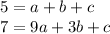
Let us eliminate c easily
2 = 8a +2b or 4a+b =1
b =1-4a
Thus parametric equation we can write as

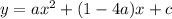
where c is arbitrary
If a>0 this will be open up otherwise open down.