Question

Show that the set of vectors {(−4,1,3),(5,1,6),(6,0,2)} does not span R 3 , but that it does span the subspace of R 3 consisting of all vectors lying in the plane with equation x + 13y − 3z = 0.

Answer 1

The vectors does not span R3 and only span a subspace of R3 which satisfies x+13y-3z=0

Step-by-step explanation:

The vectors are given as

`v_1=\left[\begin{array}{c}-4&1&3\end{array}\right] \\v_2=\left[\begin{array}{c}-5&1&6\end{array}\right] \\v_3=\left[\begin{array}{c}6&0&2\end{array}\right]`

Now if the vectors would span the
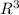`R^3`, the rank of the consolidated matrix will be 3 if it is not 3 this indicates that the vectors does not span the
`R^3`.

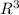So the matrix is given as

`M=\left[\begin{array}{ccc}v_1&v_2&v_3\end{array}\right] \\M=\left[\begin{array}{ccc}-4&5&6\\1&1&0\\3&6&2\end{array}\right]\\`

In order to calculate the rank, the matrix is reduced to the Row Echelon form as

`\approx \left[\begin{array}{ccc}-4&5&6\\ 0&(9)/(4)&(3)/(2)\\ 3&6&2\end{array}\right] R_2 \rightarrow R_2+(R_1)/(4)`

`\approx \left[\begin{array}{ccc}-4&5&6\\ 0&(9)/(4)&(3)/(2)\\ 0&(39)/(4)&(13)/(2)\end{array}\right] R_3 \rightarrow R_3+(3R_1)/(4)\\`

`\approx \left[\begin{array}{ccc}-4&5&6\\ 0&(39)/(4)&(13)/(2\\ 0&(9)/(4)&(3)/(2))\end{array}\right] R_2\:\leftrightarrow \:R_3`

`\approx \left[\begin{array}{ccc}-4&5&6\\ 0&(39)/(4)&(13)/(2)\\ 0&0&0\end{array}\right] R_3 \rightarrow R_3-(3R_2)/(13)\\`

As the Rank is given as number of non-zero rows in the Row echelon form which are 2 so the rank is 2.

Thus this indicates that the vectors does not span
`R^3`

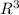
Now for any vector the corresponding equation is formulated by using the combined matrix which is given as for any arbitrary vector and the coordinate as

`v=\left[\begin{array}{c}x&y&z\end{array}\right]`

`c=\left[\begin{array}{c}c_1&c_2&c_3\end{array}\right]`

`Mc=v`

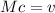
`\left[\begin{array}{ccc}-4&5&6\\1&1&0\\3&6&2\end{array}\right]\left[\begin{array}{c}c_1&c_2&c_3\end{array}\right]=\left[\begin{array}{c}x&y&z\end{array}\right]`

`M=\left[\begin{array}{ccccc}v_1&v_2&v_3& | &v\end{array}\right] \\M=\left[\begin{array}{ccccc}-4&5&6&|&x\\1&1&0&|&y\\3&6&2&|&z\end{array}\right]\\`

Now converting the combined matrix as

`\approx \left[\begin{array}{ccccc}-4&5&6&|&x\\ 0&(9)/(4)&(3)/(2)&|&(4y+x)/(4)\\ 3&6&2&|&z\end{array}\right] R_2 \rightarrow R_2+(R_1)/(4)\\`

`\approx \left[\begin{array}{ccccc}-4&5&6&|&x\\ 0&(9)/(4)&(3)/(2)&|&(4y+x)/(4)\\ 0&(39)/(4)&(13)/(2)&|&(4z+3x)/(4)\end{array}\right] R_3 \rightarrow R_3+(3R_1)/(4)\\`

`\approx \left[\begin{array}{ccccc}-4&5&6&|&x\\ 0&(39)/(4)&(13)/(2)&|&(4z+3x)/(4)\\ 0&(9)/(4)&(3)/(2)&|&(4y+x)/(4)\end{array}\right] R_3 \leftrightarrow R_2\\`

`\approx \left[\begin{array}{ccccc}-4&5&6&|&x\\ 0&(39)/(4)&(13)/(2)&|&(4z+3x)/(4)\\ 0&0&0&|&(13y+x-3z)/(13)\end{array}\right] R_3 \rightarrow R_3-(3R_2)/(13)\\`

From this it is seen that whatever the values of the coordinates does not effect the value of the plane with equation as

`(13y+x-3z)/(13)=0\\or\\13y+x-3z=0\\`

So it is verified that the subspace of R3 such that it satisfies x+13y-3z=0 consists of all vectors.