Question

If gas in a cylinder is maintained at a constant temperature​ T, the pressure P is related to the volume V by a formula of the form
`P = (nRT)/(V - nb) - (an^2)/(V^2)`.

Answer 1

The given question is incomplete. The complete question is as follows.

If gas in a cylinder is maintained at a constant temperature T, the pressure P is related to the volume V by a formula of the form

P =
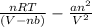`(nRT)/((V - nb)) - (an^2)/(V^2)`, in which a, b, n, and R are constants. Find
`(dP)/(dV)`.

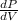Step-by-step explanation:

We will use the quotient rule for each of the two terms on the right side as follows.

P =
`(nRT)/(V - nb) - (an^(2))/(V^(2))`

`(dP)/(dV) = (0(V - nb) - nRT(1))/((V - nb)^(2)) - (0(V)^(2) - an^(2)(2V))/(V^(4))`

=
`(-nRT)/((V - nb)^(2)) - (-2an^(2)V)/(V^(4))`

=
`(-nRT)/((V - nb)^(2)) + (2an^(2))/(V^(3))`

=
`(2an^(2))/(V^(3)) - (nRT)/((V - nb)^(2))`

`(dP)/(dV) = (2an^(2))/(V^(3)) - (nRT)/((V - nb)^(2))`

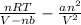
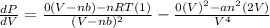
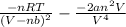
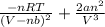
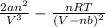
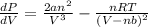
Thus, we can conclude that the value of
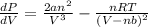`(dP)/(dV) = (2an^(2))/(V^(3)) - (nRT)/((V - nb)^(2))`.