Answer:
Part a: The two hypotheses are
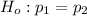 and
and
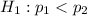 .
.
Part b: The Null hypothesis is rejected and Vaccines appear effective
Part c: As in this case the null hypothesis is rejected in the part b, thus the only possibility of error is type I error.
Part d:Children will get a vaccine which is not effective.
Step-by-step explanation:
Part a:
The two hypothesis will be tested as indicated as null hypothesis and alternative hypothesis
The null Hypothesis is given as that the population proportion for both the groups is same such that
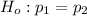
The alternative hypothesis is the percentage of people who have got vaccination is less than those who have not got the vaccination such that
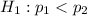
So the two hypotheses are
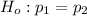 and
and
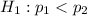 .
.
Part b:
The confidence interval in the exercise 33 is calculated as (-0.008,-0.0470) as it does not contain the value of zero thus the difference is present which indicates that the two proportions are not same
Thus the Null hypothesis is rejected and Vaccines appear effective.
Part c:
There are two types of errors as
Type I where the null hypothesis H_o is wrongly rejected and it is true.
Type II where the null hypothesis H_o is not rejected and it is false.
As in this case the null hypothesis is rejected in the part b, thus the only possibility of error is type I error.
Part d:
If the conclusion is wrong this indicates that the null hypothesis was true. i.e. There is no difference in population percentage of children with or without vaccination. This means that children will get a vaccine which is not effective.