Question

Find the matrix B of T with respect to the basis B = {~u1, ~u2}, where u1 is a unit vector that points along y = x toward increasing x and y and ~u2 is a unit vector that is perpendicular to ~u1 and 90 degrees counterclockwise from ~u1.

Answer 1

The matrix B is given as

`B=\left[\begin{array}{cc}(1)/(√(2))&-(1)/(√(2))\\(1)/(√(2))&-(1)/(√(2))\end{array}\right]`

Explanation:

As the vectors are given by u1 and u2 where u1 is given as

As y=x thus
`\theta=tan^(-1)((y)/(x))=tan^(-1){1}=\pi/4\\\\`

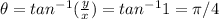
So the value of x and y is given as

Thus u_1 is given as

`u_1=\left[\begin{array}{c}(1)/(√(2))\\(1)/(√(2))\end{array}\right]`

Now the vector u_2 is given as perpendicular to u_1 i.e.

`u_1.u_2=0\\\left[\begin{array}{c}(1)/(√(2))\\(1)/(√(2))\end{array}\right].\left[\begin{array}{c}u_(2x)\\u_(2y)}\end{array}\right]=0\\u_(2x)=-(1)/(√(2))\\u_(2y)=-(1)/(√(2))\\\\u_2=\left[\begin{array}{c}-(1)/(√(2))\\-(1)/(√(2))\end{array}\right]`

So the B matrix is given as

`B=\left[\begin{array}{cc}(1)/(√(2))&-(1)/(√(2))\\(1)/(√(2))&-(1)/(√(2))\end{array}\right]`

So the matrix B is as above.