Question

A box contains two biased coins. One coin shows heads with probability 2/3, and tails with probability 1/3. The other coin shows heads with probability 1/3, and tails with probability 2/3.

a) Suppose you pick a coin at random from the box and flip it ten times and obtain 7 heads and 3 tails. What is the probability you picked the coin that is biased towards heads?
b) Suppose you pick a coin at random from the box and flip it 100 times and obtain 52 heads and 48 tails. What is the probability you picked the coin that is biased towards heads? (Note: you should get the same result as in part (a)!)

Answer 1

Explanation:

Coin I P(H) = 2/3 and P(T) = 1/3

Coin 2 P(H) = 1/3 and P(T) =2/3

Selecting one coin is equally likely with p = 0.5 each

a) you pick a coin at random from the box and flip it ten times and obtain 7 heads and 3 tails

Coin 1 : 7 heads and 3 tails probability =
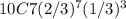`10C7(2/3)^7 (1/3)^3` ... i

coin 2 : 7 heads and 3 tails
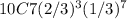`10C7(2/3)^3 (1/3)^7` ... ii

Using bayes theorem we get

the probability you picked the coin that is biased towards heads/7 heads and 3 tails occurred =(i)/(i)+(iii)

=0.9412(using Baye theorem)

b) Here we have 100 times with 52 heads and 48 tails

Coin 1: 52 H and 48 tails= 100C52 (2/3)^52 (1/3)^48

Coin 2 100C52 (1/3)^52 (2/3)^48

Use Bayes theorem to get

Required prob =2^52 /(2^52+2^48)

= 0.9412

(we get the same answer)