Answer:
Explanation:
Given that during the period from 1790 to 1930, the US population P(t) (t in years) grew from 3.9 million to 123.2 million. Throughout this period, P(t) remained close to the solution of the initial value problem.
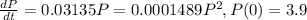
a) 1930 population is the population at time t = 40 years taking base year as 40
We can solve the differential equation using separation of variables

Resolve into partial fractions

Integrate to get
ln P -0.00474/0.0001489 (ln (0.0001489P-0.03135) = t+C
ln P -31.833 (ln (0.0001489P-0.03135) =t+C
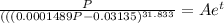
Limiting population would be infinity.