Step-by-step explanation:
Formula which holds true for a leans with radii
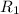 and
and
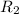 and index refraction n is given as follows.
and index refraction n is given as follows.
![(1)/(f) = (n - 1) [(1)/(R_(1)) - (1)/(R_(2))]](https://img.qammunity.org/2021/formulas/physics/college/tcrx14r22jursp5uev9ridovde5m36fv24.png)
Since, the lens is immersed in liquid with index of refraction
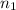 . Therefore, focal length obeys the following.
. Therefore, focal length obeys the following.
![(1)/(f_(1)) = (n - n_(1))/(n_(1)) [(1)/(R_(1)) - (1)/(R_(2))]](https://img.qammunity.org/2021/formulas/physics/college/ppw2la5wdaxeexwhtbpvas9kig9dnk5hed.png)
![(1)/(f(n - 1)) = [(1)/(R_(1)) - (1)/(R_(2))]](https://img.qammunity.org/2021/formulas/physics/college/5n68bshkd9ye7jz6buax9519nyrs4cvepw.png)
and,
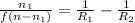
or,
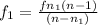
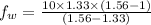
= 32.4 cm
Using thin lens equation, we will find the focal length as follows.

Hence, image distance can be calculated as follows.
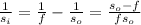
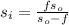
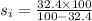
= 47.9 cm
Therefore, we can conclude that the focal length of the lens in water is 47.9 cm.