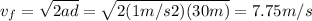Question

Two boats are separated by a distance of 60 meters. The boats start a rest and accelerate towards each other at a constant rate of 1 m/s2.

A dolphin starts mid-way between the two boats, swimming from one boat to the other at a constant speed of 14 m/s. The dolphin continues swimming back and forth between the boats until the boats crash together.


What is the total distance the dolphin travelled?

What is the speed of the boats when they crash together?

Answer 1

`D=108.5m\\v_f=7.75m/s`

Step-by-step explanation:

Let's calculate how long it takes for the boats to crash into each other. Since the problem is symmetric (the boats will meet in the middle) we want to calculate how long it takes for a boat starting from rest (
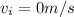`v_i=0m/s`) with
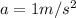`a=1m/s^2` to travel
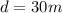`d=30m`, so we use
`d=v_it+(at^2)/(2)`:

`t=\sqrt{(2d)/(a)}=\sqrt{(2(30m))/((1m/s^2))}=7.75s`

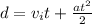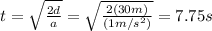
We calculate now the total distance D the dolphin traveled on this time at constant
`v=14m/s`:

`D=vt=(14m/s)(7.75s)=108.5m`

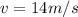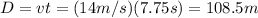
And calculate the final spead of each boat using
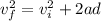`v_f^2=v_i^2+2ad`:

`v_f=√(2ad)=√(2(1m/s2)(30m))=7.75m/s`