Question

An excited electron in an Na atom emits radiation at a wavelength 589 nm and returns to the ground state. If the mean time for the transition is about 20 ns, calculate the inherent width in the emission line. What is the length of the photon emitted

Answer 1

Answer: Inherent width in the emission line: 9.20 × 10⁻¹⁵ m or 9.20 fm

length of the photon emitted: 6.0 m

Explanation:

The emitted wavelength is 589 nm and the transition time is ∆t = 20 ns.

Recall the Heisenberg's uncertainty principle:-

∆t∆E ≈ h ( Planck's Constant)

The transition time ∆t corresponds to the energy that is ∆E

`E=h/t = ((1/2\pi)*6.626*10x^(-34) J.s)/(20*10x^(-9) ) = 5.273*10x^(-27) J = 3.29* 10^(-8) eV`.

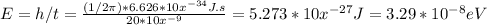The corresponding uncertainty in the emitted frequency ∆v is:

∆v= ∆E/h = (5.273*10^-27 J)/(6.626*10^ J.s)= 7.958 × 10^6 s^-1

To find the corresponding spread in wavelength and hence the line width ∆λ, we can differentiate

λ = c/v

dλ/dv = -c/v² = -λ²/c

Therefore,

∆λ = (λ²/c)*(∆v) = {(589*10⁻⁹ m)²/(3.0*10⁸ m/s)} * (7.958*10⁶ s⁻¹)

= 9.20 × 10⁻¹⁵ m or 9.20 fm

The length of the photon (l) is

l = (light velocity) × (emission duration)

= (3.0 × 10⁸ m/s)(20 × 10⁻⁹ s) = 6.0 m