Question

A light ray traveling through a material with an index of refraction of 1.2 is incident on a material that has an index of refraction of 1.4. Compared to the incident angle, the refracted angle of the light ray is

Answer 1

compared to the incident angle, the refracted angle is 45.56⁰

Step-by-step explanation:

From Snell's law;

n₁sin(I) = n₂sin(r)

Where;

n₁ is the refractive index of light in medium 1 = 1.2

n₂ is the refractive index of light in medium 2 = 1.4

I is the incident angle

r is the refractive angle

`n = (1)/(sin(I))\\\\sin(I) = (1)/(n)\\\\sin(I) =(1)/(1.2)\\\\sin(I) =0.8333\\\\I = sin^-{(0.8333)`

I = 56.439⁰

Applying snell's law

`n_1sin(I) = n_2sin(r)\\\\sin(r) = (n_1sin(I) )/(n_2)\\\\sin(r) = (1.2*sin(56.439) )/(1.4)\\\\sin(r) = 0.714\\\\r = sin^-(0.714)\\\\r = 45.56^o`

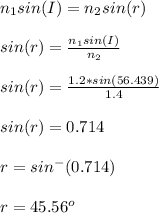
Therefore, compared to the incident angle, the refracted angle is 45.56⁰