Question

Jean Clark is the manager of the Midtown Safeway Grocery Store. She now needs to replenish her supply of strawberries. Her regular supplier can provide as many cases as she wants. However, because these strawberries already are very ripe, she will need to sell them tomorrow and then discard any that remain unsold. Jean estimates that she will be able to sell 10, 11, 12, or 13 cases tomorrow. She can purchase the strawberries for $3 per case and sell them for $8 per case. Jean now needs to decide how many cases to purchase.

Jean has checked the store’s records on daily sales of strawberries. On this basis, she estimates that the prior probabilities are 0.2, 0.4, 0.3, and 0.1 for being able to sell 10, 11, 12, and 13 cases of strawberries tomorrow.

1. What are decision variables and what are the states of nature in this problem?

2. Draw and upload the payoff table for this problem. (NOTE: You can draw the table either using software (e.g., Microsoft Paint, PowerPoint) or on a piece of paper and take a picture.)

3. If Jean wants to follow the maximin criterion, what should she do and why?

4. How many cases should Jean order if she follows the maximum likelihood criterion? Why?

5. How many cases should Jean order if she follows Bayes' decision rule and why?

6. What's the most Jean should be willing to spend to get more information about how many cases of strawberries she might be able to sell tomorrow?

Answer 1

Part 1: As a store manager, Jean Clark has to take decision regarding how many cases of strawberries should be purchased. Let Ai represents course of actions regarding how many cases to be purchased, where i = 10, 11, 12, or 13 cases.Jean has identified state of nature or circumstances for the demand of the strawberries per cases in future. Let Sj represents various demand in future, where i = 10, 11, 12, and 13 cases.

Part 2: The payoff table is attached.

Part 3: As the alternative of purchasing maximizes the minimum payoff among all events, Jane should select alternative of purchasing 10 cases of strawberries for tomorrow.

Part 4: According to the equal likelihood Principle, the alternative of purchasing 12 cases gives maximum expected value, thus Jane should purchase 12 cases of strawberries.

Part 5: The maximum EP is $53.6 for the alternative of purchasing 12 cases, thus Jane should purchase 12 cases of strawberries.

Part 6: Jean should spend $3 to get more information about how many cases of strawberries she might be able to sell tomorrow.

Step-by-step explanation:

Part 1

As a store manager, Jean Clark has to take decision regarding how many cases of strawberries should be purchased. Let Ai represents course of actions regarding how many cases to be purchased, where i = 10, 11, 12, or 13 cases.

Jean has identified state of nature or circumstances for the demand of the strawberries per cases in future. Let Sj represents various demand in future, where i = 10, 11, 12, and 13 cases.

Part 2:

`Price_(purchase\, per \,case) = \$3\\Price_(selling\, per \,case) = \$8\\ Value_(salvage) = \$0\\`

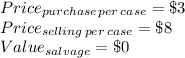
Payoff in terms of profit or loss function is determined as follows:

`Payoff = Profit_( per case) * cases_( sold )-Price_(purchase) * cases_( unsold)\\Payoff = \$5 * cases_( sold) -\ $3 * cases_(unsold)`

The payoff table is obtained using the above formulas and is attached.

Part 3:

Maximin Decision Rule:

This approach selects the alternative which maximizes the minimum payoff among all events.

Minimum payoffs of purchasing 10, 11, 12, 13 cases are $50, $47, $44, and $41 respectively.

Maximum payoff among the alternative minimum payoffs is $50 for the alternative of purchasing 10 cases.

As the alternative of purchasing maximizes the minimum payoff among all events, Jane should select alternative of purchasing 10 cases of strawberries for tomorrow.

Part 4:

Equal Likelihood Principle

This principle is based on a simple philosophy that if there is uncertainty about various events, then treat them as equally probable to occur, that is, each state of nature or chance event is assigned an equal probability. It is also known as equal probabilities criterion. In this assumption, the expected value (EV) or average payoff for each course of action or strategy is determined and the strategy with the highest mean value is adopted.

`EV_(10 cases) = [(0.5 * \$50) + (0.5 * \$50) + (0.5 * \$50) + (0.5* \$50) = \$50\\EV_(11 cases) = [(0.5 * \$47) + (0.5 * \$55) + (0.5* \$55) + (0.5 * \$55) = \$53`

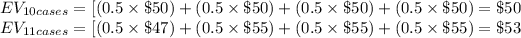
Similarly,

EV of purchasing 12 cases = $54

EV of purchasing 13 cases = $53

Maximum EV = maximize [$50, $53, $54, $53] = $54

According to the equal likelihood Principle, the alternative of purchasing 12 cases gives maximum expected value, thus Jane should purchase 12 cases of strawberries.

Part 5:

Bayes’ Decision rule

This rule considers the prior probabilities for the state of natures and selects the alternative with the maximum expected payoff. Expected payoff is calculated as sum of product of probabilities and payoff of each alternative.

Expected payoff pd purchasing 10 cases are as follows:

`EP _(10 cases) = 0.2 * \$ 50 + 0.4 * \$ 50 +0.3 * \$ 50 + 0.1 * \$ 50 = \$50\\EP_(11 cases) = (0.2 * \$47) + (0.4 * \$55) + (0.3 * \$55) + (0.1 * \$55) = \$53.4`

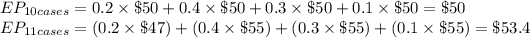
EP (12 cases) = $53.6

EP (13 cases) = $51.4

The maximum EP is $53.6 for the alternative of purchasing 12 cases, thus Jane should purchase 12 cases of strawberries.

Part 6:

To determine the cost Jane should determine Expected value of perfect information (EVPI), as follows:

First determine Expected value with perfect information (EVwPI) as follows:

Maximum payoff when demand is exactly 10 cases is $50, Expected payoff = 0.2 x 50 = $10

Maximum payoff when demand is exactly 11 cases is $55, Expected payoff = 0.4 x 55 = $22

Maximum payoff when demand is exactly 12 cases is $60, Expected payoff = 0.3 x 60 = $18

Maximum payoff when demand is exactly 13 cases is $65, Expected payoff = 0.1 x 65 = $6.5

EVwPI = $10 + $22 + $18 + $6.5 = $56.5

Expected value without perfect information (EVwoPI) = Maximum expected value by Baye’s rule = $53.6

EVPI = EVwPI – EVwoPI = $56.5 – $53.5 = $3

Jean should spend $3 to get more information about how many cases of strawberries she might be able to sell tomorrow.