Question

One of three machines must be purchased to meet an immediate need in company ACME. ACME uses a MARR of 10% in its analysis. Machine A costs 45,000 to install and will cost 9000 each year to run. Machine B has an operating cost of 9500 annually and costs 32,000 to install. Machine C can be bought for 51,000 and costs 7200 to run each year. All machines are expected to run for 8 years but only Machine C has a salvage value of 4,000. Using incremental ROR methods, identify the best economic choice.

Answer 1

Machine A $ 93,014.34

Machine B $ 82,681.80

Machine C $ 87.545,44‬

Machine B would be the best option as their net worth is lower.

Step-by-step explanation:

We calcualte the present valeu of the maintenance cost like they were annuities. Then, we add the cost for the machine. in the case of machine C we will discount the salvage value

we will pick the lower of the cost.

Machine A

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 9,000.00

time 8

rate 0.1

`9000 * (1-(1+0.1)^(-8) )/(0.1) = PV\\`

PV $48,014.3358

+ cost 45,000

net worth $ 93,014.34

machine B

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 9,500.00

time 8

rate 0.1

`9500 * (1-(1+0.1)^(-8) )/(0.1) = PV\\`

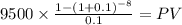
PV $50,681.7989

+ 32,000 cost

net worth: 82,681.80

machine C

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 7,200.00

time 8

rate 0.1

`7200 * (1-(1+0.1)^(-8) )/(0.1) = PV\\`

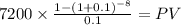
PV $38,411.4686

salvage value

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $4,000.0000

time 8.00

rate 0.10000

`(4000)/((1 + 0.1)^(8) ) = PV`

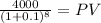
PV 1,866.0295

cost: 51,000

net worth: 51,000 + 38,411.47 - 1,866.03 = 87.545,44‬