Question

Newton's law of cooling gives the temperature T(t) of an object at time t as where and Consider the following scenario: Use Matlab to do the following: Determine the value of k. Determine the time of death, assuming that victim's body temperature was normal ( 98.6° F) prior to death, and that the room temperature was constant at 69° F. Calculate the temperature of the body for every minute between 9:18 PM and 10:18 PM Plot the temperature of the body for every minute between 9:18 PM and 10:18 PM. Include a plot title and axis labels.

Answer 1

The code as well as the outputs are presented in the parts respectively.

Step-by-step explanation:

As the question is not complete, the complete question is as attached in the figure.

The matlab code is as given below

Part a:

The Newton's Law is given as

`T(t)=T_s+(T_o-T_s)e^(-kt)`

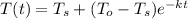
Rearranging this equation gives

`e^(-kt)=(T(t)-T_s)/(T_o-T_s)`

or

`-kt=ln((T(t)-T_s)/(T_o-T_s))`

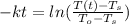
For this case the values are given as below:

T(10:18pm)= 78 F

T(9:18pm)= 79.5 F

T_s=69 F

t=1 hour

So the value of k is calculated as per following

Code:

%% For estimating the value of k

T_t=78;T_o=79.5;T_s=69;t=1; %initializing the variables

k=-(log((T_t-T_s)/(T_o-T_s)))/t;% Calculating the value of t in hr^-1

disp(['The value of k is ',num2str(k),' 1/hr'])

Output:

The value of k is 0.15415 1/hr

Part b:

For calculation of time of death following data is used

T(9:18pm)= 79.5 F

T(0)=98.6 F

T_s=69 F

k=0.15415 1/hr

Code:

%% For estimating the time of death

T_o=98.6;T_t=79.5;T_s=69; %initializing the variables

t=-(log((T_t-T_s)/(T_o-T_s)))/k;% Calculating the value of t in hr^-1

t_n=(9+12)+(18/60);%converting the time 9:18 pm into 24-hours format

t_i=t_n-t%finding the time of death in 24-hours format

t_ih=floor(t_i)%Converting time to HH:MM format (hours)

t_im=ceil((t_i-t_ih)*60)%Converting time to HH:MM format (mins)

if (t_ih)>=12%Converting time to AM/PM format

t_ih=t_ih-12;

s=' PM'

else

t_ih=t_ih;

s=' AM'

end

disp(['The time of death is ',num2str(t_ih),':',num2str(t_im),s])

Output:

The time of death is 2:35 PM

Part c:

For calculation of temperature between 9:18 PM and 10:18 PM following data is used

T_0= 79.5 F

T_s=69 F

k=0.15415 1/hr

Code:

%% Calculating value of temperature for each minute between 9:18 PM and 10:18 PM

T_o=79.5;T_s=69; %initializing the variables

t=1/60; %Converting a minute to hour

T=zeros(60,1);%Initializing the array to store the temperature

e=exp(1);

for i=1:1:60%counter for an hour

T(i,1)=T_s+(T_o-T_s)*e^(-k*t);%Estimating the temperature after 1 min

T_o=T(i,1);%Changing the T_o

end

disp('The temperature variation with time in mins is as below')

T

Output:

The temperature variation with time in mins is as below

T =

79.4731

79.4462

79.4194

79.3926

79.3660

79.3394

79.3129

79.2864

79.2600

79.2337

79.2074

79.1812

79.1551

79.1290

79.1031

79.0771

79.0513

79.0255

78.9998

78.9741

78.9485

78.9230

78.8975

78.8721

78.8468

78.8215

78.7963

78.7712

78.7461

78.7211

78.6962

78.6713

78.6465

78.6217

78.5970

78.5724

78.5478

78.5233

78.4989

78.4745

78.4502

78.4260

78.4018

78.3777

78.3536

78.3296

78.3057

78.2818

78.2580

78.2342

78.2105

78.1869

78.1633

78.1398

78.1164

78.0930

78.0696

78.0464

78.0232

78.0000

Part d:

The plot is as attached.

Code:

%% Plotting the temperature profile

t=1:1:60;

plot(t,T,'-o')

xlabel('Time between 9:18 PM and 10:18 PM in mins')

ylabel('Temperature of body in F')

title('The variation of body temperature between 9:18 PM & 10:18 PM')

grid on

The output is also attached in the file