Question

The multiple regression equation is much better. 3. Predict the total packing cost for 25,000 orders, weighing 40,000 pounds, with 4,000 fragile items. Round regression intercept to whole dollar and coefficients to two decimal places (nearest cent). Enter the final answer rounded to the nearest dollar. Y = $ 4. How much would the cost estimated for Requirement 3 change if the 25,000 orders weighed 40,000 pounds, but only 2,000 were fragile items? In your computations, round regression intercept to whole dollar and coefficients to two decimal places (nearest cent). Enter the final answer rounded to the nearest dollar. The new total packing cost would be: $

Answer 1

Part 3: The packaging cost for 25000 orders of weight 40,000 pounds with 4000 fragile items is $ 91999.

Part 4: The packaging cost for 25000 orders of weight 40,000 pounds with 2000 fragile items as compared to the cost with 4000 fragile items is reduced by $ 4626.

Step-by-step explanation:

The question lacks the data. So the data is given as in the attached figure which indicates following.

From the part 2 of the question the regression line is found as

`Cost_(packing) = 475 + 2.100n_(order) + 0.7443w_(order)+2.313n_(fragile)`

Part 3

Number of orders=25000

Weights=40,000

Number of fragile items=4000

So the value is predicted as

`Cost_(packing) = 475 + 2.100n_(order) + 0.7443w_(order)+2.313n_(fragile)\\Cost_(packing) = 475 + 2.100(25000)+ 0.7443(40000)+2.313(4000)\\Cost_(packing) = \$ 91999`

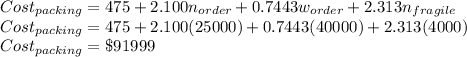
So the packaging cost for 25000 orders of weight 40,000 pounds with 4000 fragile items is $ 91999.

Part 4

Part 3

Number of orders=25000

Weights=40,000

Number of fragile items=2000

So the value is predicted as

`Cost_(packing) = 475 + 2.100n_(order) + 0.7443w_(order)+2.313n_(fragile)\\Cost_(packing) = 475 + 2.100(25000)+ 0.7443(40000)+2.313(2000)\\Cost_(packing) = \$ 87373`

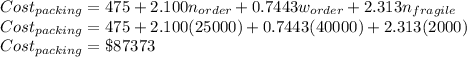
Change in cost is

`\Delta Cost=Cost_3-Cost_4\\\Delta Cost=91999-87373\\\Delta Cost=$4626\\`

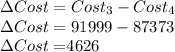
So the packaging cost for 25000 orders of weight 40,000 pounds with 2000 fragile items as compared to the cost with 4000 fragile items is reduced by $ 4626.