Question

Let f (x )equals StartFraction StartAbsoluteValue x EndAbsoluteValue Over x EndFraction . Then ​f(minus​2)equalsminus1 and ​f(2)equals1. ​Therefore, ​f(minus​2)less than0less than​f(2) but there is no value of c between minus2 and 2 for which ​f(c)equals0. Does this fact violate the intermediate value​ theorem? Explain.

Answer 1

Explanation:

Given that

`f(x) = (|x|)/(x)`

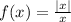
f(-2) = 1 and f(2) = 1

The question is here we have values for -1 and 1 the same and hence we must get a c such that f(c) =0

Because we are not getting here c value does it violate the intermedate value theorem

Please go through the conditions for intermediate theorem to be valid

If f(x) is continuous in the interval [a,b] and f is differentiable in the interval (a,b) and if f(b) = f(a) then we have a c in the interval (a,b) such that f(c) = 0

But our f(x) is not differntiable in the interval (-2,2) because at x =0 we get left derivative =-1 and right derivative =1

So f is not differntiable in the interval.

Hence intermediate theorem cannot be applied here.