Answer: The correct options are:
The second run will be faster.
The second run has twice the surface area.
Step-by-step explanation:
It is known that,
Reaction catalyzing power of catalyst
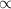 its exposed surface area
its exposed surface area
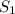 = ?,
= ?,
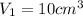 ,
,
As, area =
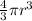
r = 1.545 cm
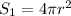
Also,
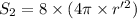
r' = ?
Hence, expression for the volume conservation will be as follows.
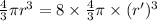
Since,
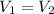
r' =
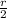
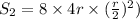
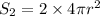
Therefore,

Thus, we can conclude that the second run will be faster and the second run has twice the surface area.