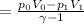Question

At the end of the adiabatic expansion, the gas fills a new volume V₁, where V₁ > V₀. Find W, the work done by the gas on the container during the expansion. Express the work in terms of p₀, V₀, and V₁. Your answer should not depend on temperature.

Answer 1

`W=(p_0V_0-p_1V_1)/(\gamma-1)`

Step-by-step explanation:

An adiabatic process refers to one where there is no exchange of heat.

The equation of state of an adiabatic process is given by,

`pV^(\gamma)=k`

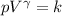
where,

`p` = pressure

`V` = volume

`\gamma=(C_p)/(C_V)`

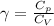
`k` = constant

Therefore, work done by the gas during expansion is,

`W=\int\limits^(V_1)_(V_0) {p} \, dV`

`=k\int\limits^(V_1)_(V_0) {V^(-\gamma)} \, dV`

`=(k)/(\gamma -1) (V_0^(1-\gamma)-V_1^(1-\gamma))\\`

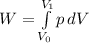
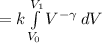
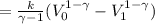
(using
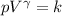`pV^(\gamma)=k` )

`=(p_0V_0-p_1V_1)/(\gamma-1)`