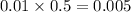Question

The specific gravity of a substance is given by G = DS/DW, where DS is the density of the substance in kg/m3 and DW is the density of water, which is known to be 1000 kg/m3. The density of a particular substance is measured to be DS = 500±5 kg/m3. Estimate the specific gravity, and find the uncertainty in the estimate

Answer 1

`G=0.5\pm0.005`

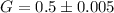
Step-by-step explanation:

The specific gravity is given by,

`G=(D_S)/(D_W)=(500)/(1000) =0.5`

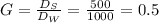
Now, in order to calculate the uncertainty (relative error) in G, we must first take log (base e) on both sides of the equation,

`lnG=ln((D_S)/(D_W) )=lnD_S-lnD_W`

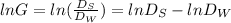
Differentiating the above equation,

`(dG)/(G)=(dD_S)/(D_S)`

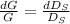
The second term is zero because it is known that
`D_W=1000kg/m^3` and hence a constant.

Putting the appropriate values, we get,

`(dG)/(G)=(dD_S)/(D_S)=(5)/(500) =0.01`

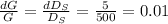
Therefore, uncertainty in G =
`0.01*0.5=0.005`