Question

Which expressions are completely factored? Select each correct answer. 32y10−24=8(4y10−3) 18y3−6y=3y(6y2−2) 16y5+12y3=4y3(4y2+3) 20y7+10y2=5y(4y6+2y) PreviousNext

Answer 1

Option A and Option C

Explanation:

Option A:
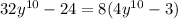`32y^(10)-24 = 8(4y^(10)-3)` This is completely factored as 8 is the Highest Common Monomial factor

Option B:
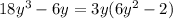`18y^(3)-6y = 3y(6y^(2)-2)` This is not completely factored as 2 is still a common factor of 6y2 and -2.

Option C:
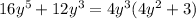`16y^(5)+12y^(3)=4y^(3)(4y^(2)+3)` This is completely factored as 4y2 is the Highest Common Monomial factor

Option D:
`20y^(7)+10y^(2) = 5y(4y^(6)+2y)` This is not completely factored as 2y is still a common factor of 4y6 and 2y.

So the options that are completely factored are Option A and Option C