Question

Bond price: Pierre Dupont just received a cash gift from his grandfather. He plans to invest in a five-year bond issued by Venice Corp. that pays an annual coupon rate of 5.5 percent. If the current market rate is 7.25 percent, what is the maximum amount Pierre should be willing to pay for this bond?

Answer 1

$929 approx

Step-by-step explanation:

Assumption: Since face value of the bond is not provided, it has been assumed to be $1000 and solved accordingly.

The present value of a bond i.e bond price is the sum total of the present value of it's future coupon payments in addition to redemption value, both discounted at yield to maturity rate. It is expressed as

`B_(0) = (C)/((1\ +\ YTM)^(1) ) \ +\ (C)/((1\ +\ YTM)^(2) ) \ +.....+\ (C)/((1\ +\ YTM)^(n) ) \ +\ (RV)/((1\ + YTM)^(n) )`

where,
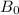`B_(0)` = Present Value of the bond

C = Annual coupon payment

YTM = Yield to maturity rate

n = No of years to maturity.

Here, C = $55 (assumed par value of each bond as $1000)

YTM = 7.25% per annum

n = 5 years

Putting these values in above equation, we get,

`B_(0) = (55)/((1\ +\ .0725)^(1) ) \ +\ (55)/((1\ +\ .0725)^(2) ) \ +.....+\ (55)/((1\ +\ .0725)^(5) ) \ +\ (1000)/((1\ + .0725)^(5) )`

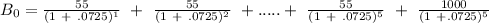
Hence, 4.073 × 55 + 1000 × 0.7047

= $929 approx

Hence, Pierre should pay less than it's face value for such a bond.