a) See free-body diagram in attachment
b)
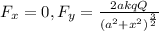
c)
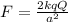
Step-by-step explanation:
a)
The free-body diagram of the situation can be found in attachment.
We have:
- The charge of +q is located at y = a
- The charge of -q is located at y = -a
- The charge -Q is located at x = a
We observe that:
- The force exerted by charge +q on charge -Q is attractive, since the two charges have opposite sign, so it points to the north-west direction
- The force exerted by charge -q on charge -Q is repulsive, since the two charges have same sign, so it points to the north-east direction
So, the net force points north.
b)
We start by evaluating the situation on the x-direction first.
We observe that:
- The two charges +q and -q have same magnitude
- Also, they are located at exactly same distance from charge -Q
This means that the x-components of the force that each charge exerts on -Q are equal, but opposite in direction: therefore, they cancel each other, so the net force on the x-direction is zero:
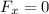
Instead, we observe that the y-components of the force that each charge exerts on -Q are both upward, therefore they add together.
The distance between charge +q and charge -Q is:

where x is the location of the charge -Q.
The force between any of the two charges q, -q and charge -Q is given by (magnitude):
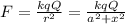
However, we are only interested in the y-component of the force, which is given by
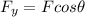
where
 is the angle between
is the angle between
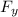 and
and
 . By using trigonometry,
. By using trigonometry,

So, substituting into the equation for
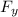 , we find
, we find
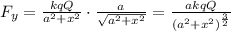
However, the net force is the sum of the forces due to the 2 charges, so
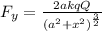
c)
Here we want to find the net force on the charge -Q when this is located at the origin, so when
x = 0
We already said that the net force on the x-direction is always zero, so
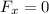
Instead the net force on the y-direction is given by
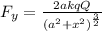
Therefore, by substituting x = 0, we find:

And the net force is in the upward direction, towards charge +q.