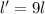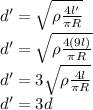Answer:
three times the original diameter
Step-by-step explanation:
From the wire's resistance formula, we can calculate the relation between the diameter of the wire and its length:
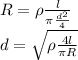
Here, d is the wire's diameter,
 is the electrical resistivity of the material and R is the resistance of the wire. We have
is the electrical resistivity of the material and R is the resistance of the wire. We have